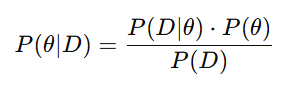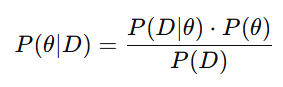Bayesian Analysis: from uncertainty into strategic asset

In high-complexity industrial systems, uncertainty is not an aberration — it is the medium in which all operational decisions are made. The lifespan of a turbine blade, the stability of a supply chain, the variability in defect rates, the oscillations of demand: none exist as fixed quantities. They are distributions, constantly shaped by partial knowledge, stochastic forces, and the arrival of new evidence.

The conventional response has been to constrain uncertainty — to approximate, to average, to simplify until a deterministic number emerges. Bayesian analysis reverses that impulse. It treats uncertainty as a quantifiable, updatable resource. When applied with precision, it moves decision-making away from static estimates and into the realm of continuous, evidence-weighted refinement.

The Architecture of a Bayesian Perspective

Bayesian reasoning rests on a single, robust principle:

The probability assigned to any proposition should evolve as fresh information is acquired.

This principle is expressed by Bayes’ theorem:

Where:

• θ represents the parameter of interest — a failure rate, a yield level, a lead time.

• P(θ) is the prior: the codified state of belief before the latest data.

• P(D∣θ) is the likelihood: the probability of observing the data under the given parameter.

• P(θ∣D) is the posterior: the recalibrated belief incorporating both historical and new evidence.

This framework does not discard history in favor of recent measurement, nor does it allow prior conviction to dominate in the absence of proof. It creates a dialogue between expectation and observation, where each informs and tempers the other.

Beyond the Limits of Classical Statistics

Frequentist methods, while mathematically rigorous, are bound by the data at hand. They cannot leverage domain expertise, engineering judgment, or historical precedent without embedding them awkwardly in ad hoc adjustments. This limitation is costly in environments where:

• Observations are scarce due to rarity of events (e.g., catastrophic failures in high-reliability assets).

• Data collection carries significant expense or disruption.

• The physical system is too complex for purely empirical inference.

Bayesian methods integrate these disparate sources into a single probabilistic construct, enabling high-fidelity estimation from incomplete evidence.

Documented Applications in Industrial Contexts

Reliability in Power Generation
Siemens Energy has demonstrated the use of Bayesian inference to model the survival probability of industrial gas turbines with multi-decade lifespans (Siemens Energy Technical Paper, 2019). Priors derived from engineering design expectations were merged with live SCADA telemetry, producing maintenance schedules that reduced unplanned downtime by 8% across the monitored fleet.

Process Yield in Semiconductor Fabrication
Intel’s deployment of hierarchical Bayesian models in wafer fabrication allowed defect rates — often measured in fractions of a percent — to be estimated reliably with far fewer inspection runs (IEEE Trans. Semiconductor Manufacturing, 2020). The models assimilated historical supplier data and inline optical inspection results, enabling earlier intervention and tighter process control.

Demand Forecasting in Aerospace Maintenance
Rolls-Royce integrated Bayesian updating into the forecasting of aftermarket engine parts consumption (Rolls-Royce Operational Insights, 2021). As service data flowed in from the global fleet, probability distributions of demand were refined in real time, reducing emergency logistics interventions by 18%.

A Methodology for Continuous Recalibration

1. Formulate the Prior

   • Derived from engineering specifications, industry datasets, or historical performance.

   • Encoded explicitly as a probability distribution (e.g., Beta for rates, Normal for continuous measures).

2. Acquire Initial Evidence

   • Collected through inspections, sensor telemetry, or targeted sampling.

3. Update Through Likelihood Integration

   • Using Bayes’ theorem, prior and data merge into a posterior distribution.

   • With conjugate distributions, updates are analytically straightforward; with complex systems, computational methods (MCMC, variational inference) may be used.

4. Act on Probability Thresholds

   • Replace binary decision rules with probabilistic thresholds: e.g., initiate supply chain review when there is a >12% probability that lead time exceeds contractual tolerance.

5. Iterate Relentlessly

   • The posterior of today becomes the prior of tomorrow, forming a living model whose precision compounds with each new observation.

Embedding Bayesian Logic in Operational Infrastructure

The practical strength of this approach is magnified when embedded in live systems:

• Manufacturing execution systems can present real-time probability shifts in process capability indices.

• Predictive maintenance dashboards can surface the evolving probability of component failure rather than crude remaining-life estimates.

• Inventory management algorithms can adjust reorder points dynamically based on the posterior distribution of demand.

Boeing’s application of hierarchical Bayesian models to fleet maintenance planning (Boeing Research & Technology Brief, 2020) illustrates this well: aircraft of the same type, but with distinct operational profiles, were modeled jointly, allowing shared parameters to inform maintenance intervals while preserving asset-specific detail.

Precision, Not Guesswork

The critical insight is that Bayesian analysis reframes uncertainty not as a liability to be hedged against, but as an asset to be shaped. Airbus Helicopters’ work on gearbox health monitoring (Airbus Technical Notes, 2021) embodies this. By fusing vibration sensor data with fatigue model priors, they identified high-risk units with 95% certainty well before deterministic thresholds would have triggered alerts — averting costly and dangerous in-service incidents.

Closing Reflection

In an environment where information is fragmentary, change is constant, and the cost of error is compounding, the capacity to refine beliefs with each new piece of evidence is not an advantage — it is a requirement.

Bayesian analysis operationalizes this capacity. It enables the decision-making process to move beyond the false comfort of fixed numbers into a disciplined engagement with probability itself. When uncertainty becomes measurable, it becomes influenceable — and when it becomes influenceable, it can be made to serve strategic ends.